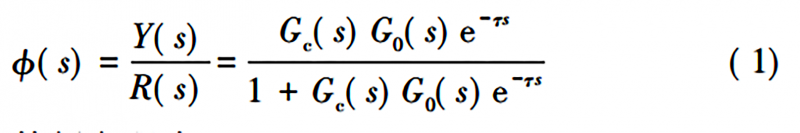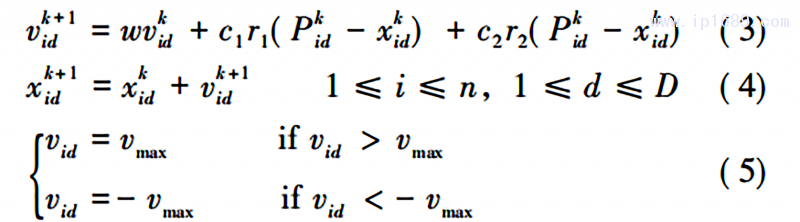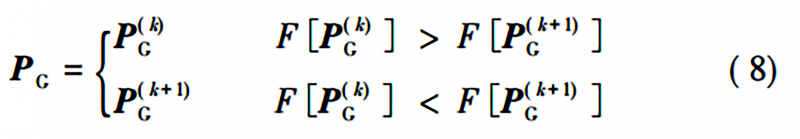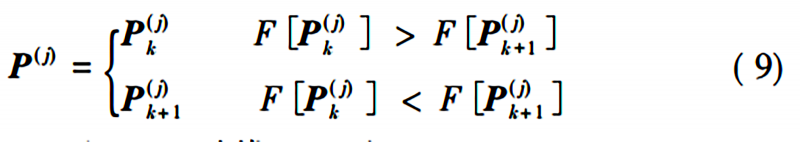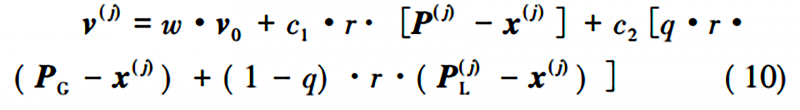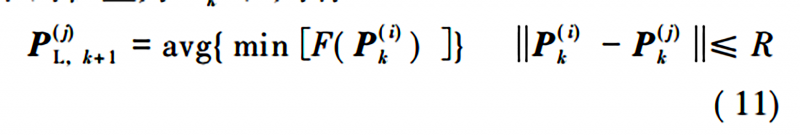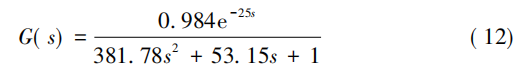周冬冬,陳明霞,趙金迪
(桂林理工大學機械與控制工程學院,廣西桂林 541006)
摘要: 為提高橡膠擠出機Smith-模糊PID溫度控制系統的控制精度,更好地實現智能整定參數與橡膠擠出機溫度最優控制,采用混合粒子群(HPSO)算法優化Smith-模糊PID控制系統,完成對溫度控制系統PID參數基準值的自動尋優。借助MATLAB軟件辨識擠出機溫控系統數學模型,搭建Smith-模糊PID溫度控制系統。為避免粒子群 (PSO)算法陷入局部最優,在PSO算法的基礎上將社會因子分解為局部社會因子和全局社會因子,設計出HPSO算法對PID參數進行尋優;將HPSO算法優化系統前后的控制效果進行對比。結果表明:采用HPSO算法優化Smith-模糊PID溫度控制系統的控制精度更高、抗干擾性能更強,溫度控制精度在±(1~1.5) ℃以內,并且接近±1℃,完全滿足橡膠擠出生產過程中對料筒溫度控制的指標要求,可以在一定程度上提升溫控系統的控制精度以及擠出機械的智能化水平。
關鍵詞: 橡膠擠出機;溫度控制系統;模糊PID控制;Smith預估;混合粒子群算法
0 前言
橡膠具有韌性高、延展性強、絕緣性好等特點,是汽車輪胎工業必不可少的原材料。橡膠擠出機是橡膠制品擠出成型過程中的核心機械設備,對其精密控制是實現擠出半成品達到高質量標準的必要途徑。擠出過程受各類波動因素的影響,其中,橡膠膠料對于溫度的變化十分敏感,因此擠出機溫度的波動會直接影響半成品物理性能,溫度過低或過高,都會導致膠料熔融效果較差,對擠出半成品的質量造成很大的影響[1]。
在實際擠出生產過程中,對膠料品質起主要影響的是擠出機料筒部分的溫控[2-3]。傳統PID料筒溫控系統控制精度低,無法解決料筒溫控過程中存在的大滯后問題,而Smith-模糊PID料筒溫控系統可以很好地解決溫控過程中的滯后問題,提高溫度控制精度。在料筒溫控過程中,PID控制器的參數有一個基準值,而模糊PID算法就是在原PID的基礎上根據誤差對PID參數基準值進行動態微調。但在控制過程中,基準值是靜態不變的,而且是通過人工經驗調節得到的,并不是最優參數。
針對上述問題,本文作者在搭建料筒Smith-模糊PID溫度控制系統的基礎上,設計一種 HPSO(Hybrid Particle Swarm Optimization)算法優化Smith-模糊PID溫度控制系統,實現智能整定 Smith-模糊PID控制器參數。將智能算法與Smith-模糊PID有效結合并應用于橡膠擠出機料筒溫度控制中,不僅解決了料筒溫控過程中存在的大滯后問題,還實現了自動尋優PID參數的基準值,提高Smith-模糊PID溫度控制系統的控制精度,實現對于擠出機料筒溫度的精密控制。
1、擠出機溫度控制系統工藝簡介
本文作者研究的主要是銷釘式冷喂料橡膠擠出機,其溫控系統由循環水管路和電控加熱器件組成。料筒中膠料的溫度主要通過電控加熱器加熱循環水來控制[4]。循環水通過加熱器加熱以后,經加壓泵供給料筒的外壁流道及螺桿冷卻孔中,實現膠料溫度的增加。料筒循環水管路如圖1所示。
圖 1 料筒管路外觀
當水溫探測器檢測到循環水溫度高于設定值時,加冷卻水進入循環熱水中,降低循環水的溫度。通過分析料筒溫度控制工藝,知道文中研究的料筒溫度控制系統的主要控制量是循環水的電加熱器功率。具體的電控系統實物結構如圖2所示。
圖 2 水循環電控系統實物結構
2、Smith- 模糊PID溫控系統搭建
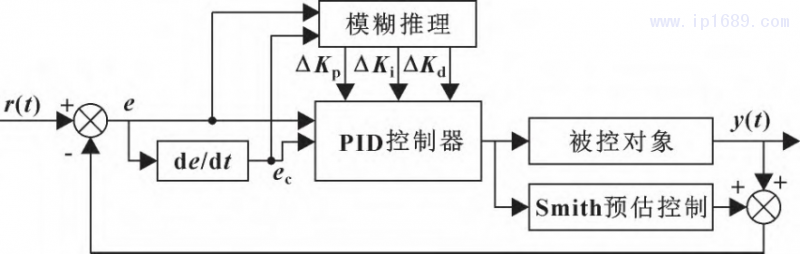
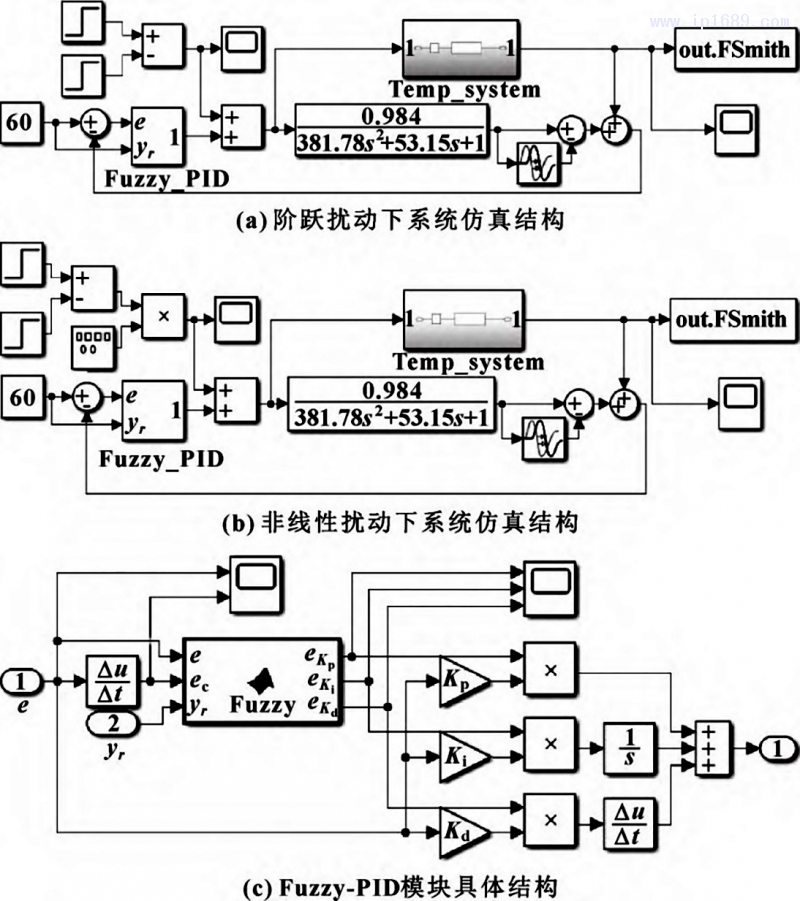
Smith-模糊PID溫控系統是在模糊PID控制系統的基礎上,加入Smith預估器,所以首先要搭建模糊PID控制器。根據料筒溫度控制工藝結合模糊控制器選型規則,模糊控制器選取二維型。r(t) 為溫度設定值,y(t)為實際檢測溫度值,兩者的偏差e和偏差變化率ec為輸入,具體結構如圖3所示。
圖 3 模糊 PID 控制原理
模糊控制器的模糊子集的符號以及對應的含義和數值如表1所示。
表 1 模糊規則中的符號含義
輸入、輸出模糊論域分別設置為 {-0.7、-0.4、-0.15、0、0.15、0.4、0.7} 、{ -0.4、-0.2、-0.1、-0.05、0、0.05、0.1、0.2、0.4} 。如圖4所示,選用三角形隸屬函數采用Mamdani推理法與重心法分別進行去模糊化和清晰化[5],模糊控制規則如表2所示。
圖 4 輸入變量的隸屬度函數
表 2 ΔKp、ΔKi、ΔKd 的模糊控制規則
在模糊PID控制器搭建完成后,繼續搭建Smith預估控制器。料筒溫控傳遞函數為
特征方程為
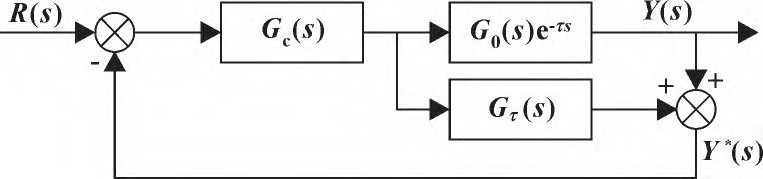
根據 Smith 滯后補償原理[6],搭建Smith預估控制器如圖5所示。有 Gτ(s)=G0(s) ( 1-e-τs) ,
Y*(s)=G0(s)。
圖 5 Smith 預估控制系統結構
將所搭建的Smith預估器加入到模糊PID控制器中,得到料筒溫度Smith-模糊PID控制系統如圖6所示[7-8]。
圖 6 Smith-模糊 PID 控制原理
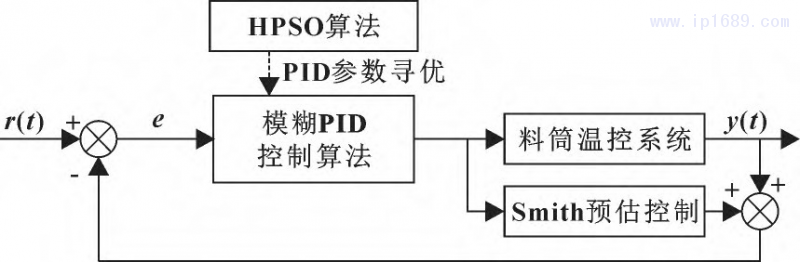
在完成Smith-模糊PID控制系統搭建后,采用HPSO算法進行優化,實現智能精準尋優PID控制參數。優化結構如圖7所示。
圖 7 HPSO-Smith 模糊 PID 料筒溫控系統結構
3 混合粒子群算法簡介
3. 1 粒子群算法描述
粒子群優化 ( Particle Swarm Optimization,PSO)是一種隨機搜索算法,在動態或者多目標優化環境中,更能發揮自身的優勢[9]。假設群體的搜索解空間為D維,種群規模為N,第i個粒子坐標為 xi =[xi1,xi2,…,xiD]T、速度為vi=[vi1,vi2,…,viD]T,第i個粒子的歷史最佳位置為Pi=[Pi1,Pi2,…,PiD]T,整個種群尋的最佳位置為Pg=[Pg1,Pg2,…,PgD]T[10]。
當搜索到以上2個最佳位置時,粒子就根據式(3) (4)更新自身的速度和位置:
式中: w 為慣性權重; k 為當前迭代次數; vid為粒子速度,vid∈[- vmax,vmax ] ; c1和c2為粒子加速常數; r1 和 r2 為 ( 0,1) 內的隨機數。
每個粒子的初速度定為0,即 v0 = 0,第j(1≤j≤ m)個粒子的下一次迭代的速度v(j)由三部分組成:
v(j) = w·v0 + c1·r·[P(j)-x(j)]+ c2·r·[PG-x(j)](6)
式中: r為( 0,1)內的隨機數; v0為上一次迭代的粒子速度; w·v0 為自身慣性因子; c1·r·[P(j)-x(j)]為自身最優因子,P(j)為第j個因子自適應度最高的位置; c2·r·[PG-x(j)]為社會因子,PG為種群中自適應度最高的位置。
對于第j個粒子,第k+1次迭代的位置 x(j)k+1與第k次迭代的位置x(j)k、速度v(j+1)k關系為
式中: dt 為仿真間隔。
記前 k 次的 PG 為 P(k)G ,第k+1次迭代中適應度最高的粒子位置記為P( k+1)G ,則最終的PG為
記前k次的第j個粒子的位置為P(j)k,第 k+1次的第j個粒子的位置為P(j)k+1,則最終的歷史最優解P(j)為
3. 2 混合粒子群算法設計
本文作者在 PSO 算法的基礎上,將PSO算法中的社會因子分解為局部社會因子和全局社會因子,即得到混合粒子群( HPSO) 算法,所以HPSO算法中粒子速度可表示[11]為
式中: 0<q<1,q為全局社會因子的占比;PG為全局最優解。P(j)與PG的計算公式在PSO算法中已給出,有所不同的是,P(j)L為第j個粒子的局部最優解坐標。
將第k次迭代的P(j)L記為P(j)L,k,第 k次迭代的第i粒子的位置為P(i)k,則有:
即在與第j個粒子的距離不超過R的所有粒子中,選擇具有最小函數值的粒子。
3. 3 混合粒子群算法優化流程
HPSO 算法優化 Smith-模糊PID控制器參數的步驟:
步驟1,確定參數維度N、慣性系數c1、c2、w、種群規模m、迭代次數n、局部因子作用半徑R;
步驟2,計算每個粒子的速度;
步驟3,計算每個粒子的自適應度 F(j)k+1 ,計算出P(j)、PG和P(j)L ;
步驟4,將上一步中的粒子依次賦值給控制器,并運行系統模型;
步驟5,輸出性能指標,判斷是否滿足控制要求,若滿足,則停止尋優; 若不滿足,則繼續尋優;
步驟 6,更新粒子群信息,重復上面步驟。
4 系統仿真
文中以循環水加熱器的電功率P為操作變量,通過循環水溫度來控制料筒溫度,所以料筒溫度T為被控變量。通過某五復合橡膠擠出機生產線現場所提供的實驗數據,利用MATLAB辨識實驗數據[12],得到料筒溫度T與電加熱器功率P的關系,即系統傳遞函數:
4. 1 干擾下Smith-模糊PID溫控系統響應
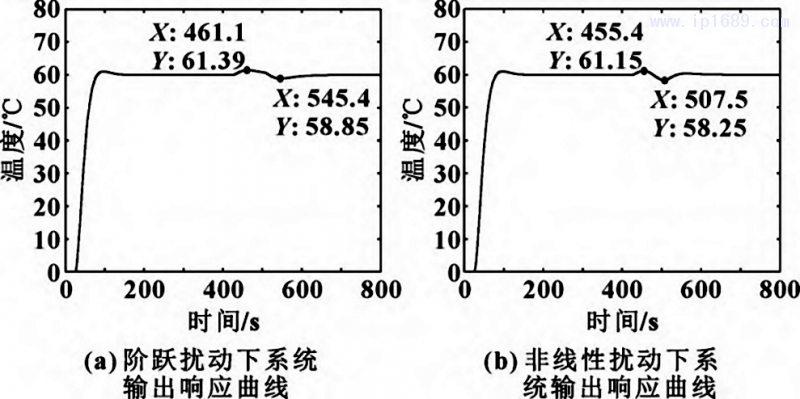
在Simulink中搭建Smith-模糊PID料筒溫度控制系統仿真模型,同時加入階躍與非線性擾動進行仿真。料筒目標溫度選取為60℃,階躍與非線性擾動信號的幅值均設置為5,擾動作用時間為 400~480;非線性正弦擾動信號頻率設置為0.05Hz,仿真結構如圖 8 所示。Smith-模糊PID料筒溫控系統輸出響應曲線如圖9所示。
圖 8 Smith-模糊 PID 料筒溫控系統仿真模型
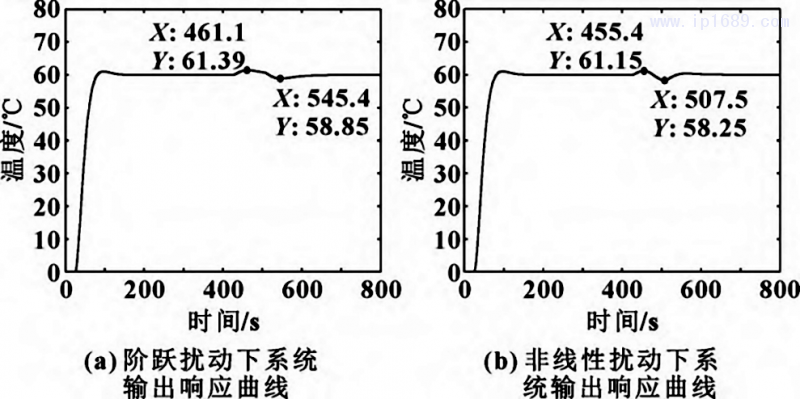
圖 9 Smith-模糊 PID 料筒溫控系統輸出響應曲線
由圖9可知:階躍與非線性干擾作用時,Smith-模糊PID料筒溫控系統響應波動幅度分別為±1.4℃和±1.8℃,在仿真進行到480s干擾作用結束時,系統基本上分別在第600s和第550s恢復到原穩定狀態。結果表明:在受到干擾作用后,Smith-模糊PID控制系統能克服擾動并快速恢復到原穩定狀態,并且溫度控制精度在±2℃以內。由于橡膠擠出工藝中料筒溫度控制性能指標要求為±( 1~1. 5)℃,所以料筒溫度 Smith-模糊PID控制系統還沒有完全達到控制精度要求,因此采用HPSO算法進一步優化。
4. 2 HPSO優化Smith-模糊PID溫控系統
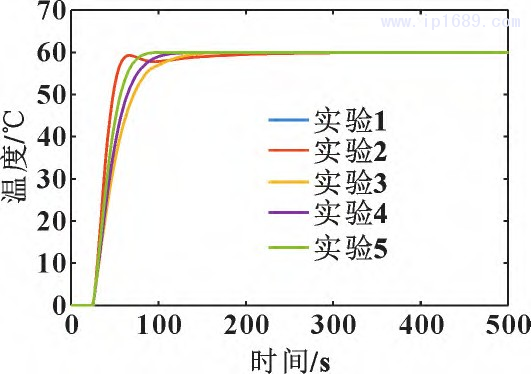
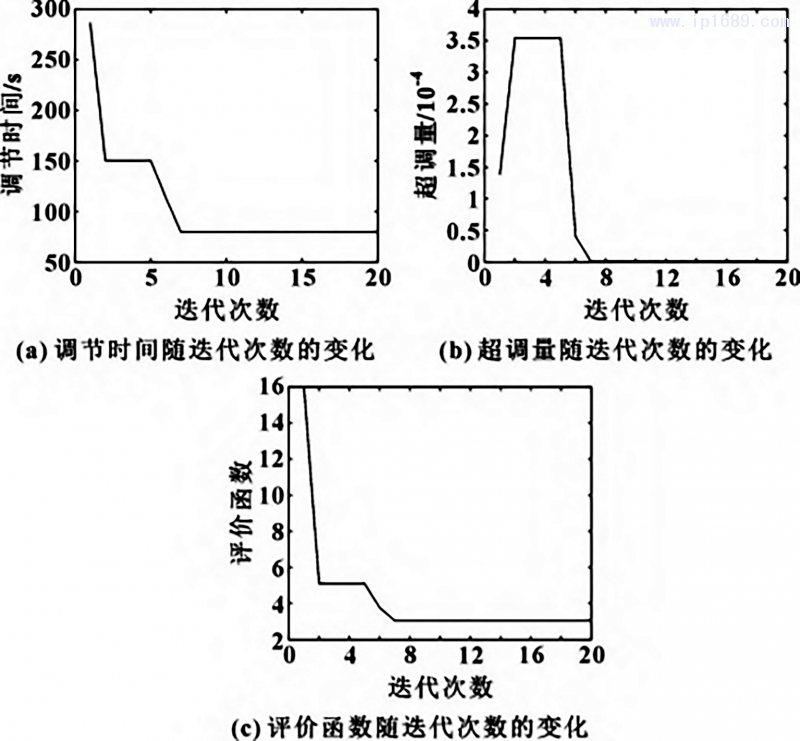
HPSO算法參數設定:種群規模為50,最大迭代次數為20,位移仿真間隔dt為0.3,w為2,c1為2,c2為2,xmax為10、0. 1、10,vmax=0. 5xmax,局部社會因子ρ為0.4,局部因子作用半徑R為0.2。進行5次仿真實驗,得到 HPSO算法優化 Smith-模糊PID控制器的響應曲線,如圖10所示。HPSO算法優化信息如圖11所示。PID參數隨迭代次數變化如圖12所示。
圖 10 HPSO 優化 Smith-模糊 PID
圖 11 HPSO 優化 Smith-模糊 PID 系統信息曲線
圖 12 PID 參數隨迭代次數的變化
由圖10可以看出:隨著迭代的進行,系統輸出響應越來越好。由圖11可以看出:迭代優化到第7次以后,調節時間穩定,而且調節時間曲線波動較少,系統無超調量且保持穩定,評價函數隨優化過程波動小并逐漸穩定。由圖12可以看出:隨著迭代優化7次后,3個參數的相對值穩定不變,最終得到HPSO優化Smith-模糊PID控制器的3個參數Kp、Ki、Kd分別為2. 657 8、0. 054 2和8. 360 4。
4. 3 HPSO 優化前后抗干擾性對比
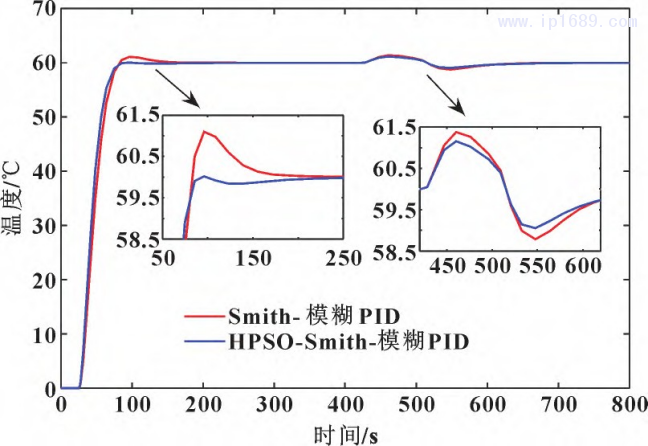
為驗證HPSO算法優化的 Smith-模糊PID系統具有更好的抗擾性能,在相同擾動情況下對比分析 HP-SO 算法優化的 Smith-模糊PID控制系統與Smith-模糊PID控制系統的抗擾性能。擾動數值設置與前面相同,得到階躍擾動下、非線性擾動下系統抗擾性輸出曲線分別如圖13和圖14所示。
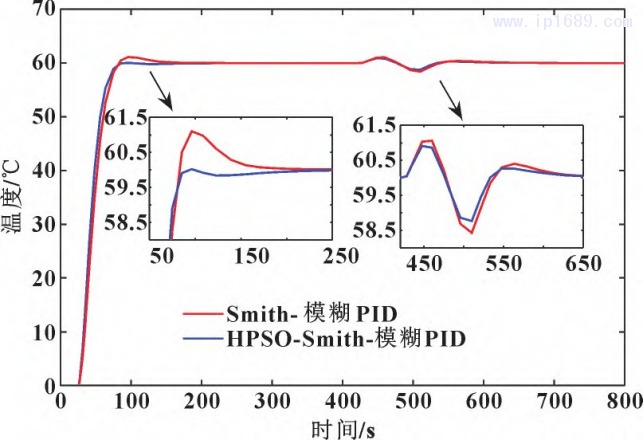
圖 13 階躍擾動下HPSO 優化 Smith- 模糊PID前后抗擾對比曲線
圖 14 非線性擾動下 HPSO 優化 Smith- 模糊PID前后抗擾對比曲線
由圖13、圖14可以看出:HPSO算法優化后的系統動態響應無超調,而優化前的系統有大約2%的動態超調;在階躍干擾作用下,優化后系統受干擾的波動幅度為±1.1℃,優化前系統受干擾的波動幅度為±1.4℃; 在非線性干擾作用下,優化后系統受干擾的波動幅度為±1.2 ℃,優化前系統受干擾的波動幅度為±1.6℃。結果表明:HPSO-Smith模糊PID控制系統的動態響應無超調、穩態誤差為零,溫度控制精度在± (1~1.5)℃以內,并且接近±1℃ ,能夠快速地跟蹤并抑制料筒溫度的變化。
5 結束語
基于Smith-模糊PID控制器,在PSO算法的基礎上設計出HPSO算法優化Smith-模糊PID控制系統,用于橡膠擠出機料筒溫度控制。HPSO算法優化后的Smith-模糊PID控制系統在動態響應與抗干擾性能方面都比Smith- 模糊PID 控制系統有所提升。采用HPSO算法完成對PID參數基準值的自動尋優,從而使系統輸出響應具有較好的動態與穩態性能。結果表明:在線性與非線性干擾作用下,HPSO算法優化的Smith-模糊PID溫度控制系統仍具有良好的魯棒性與自適應性,溫度控制精度在±(1~1.5)℃,并且接近±1℃,完全滿足橡膠擠出生產過程中對料筒溫度控制的指標要求,能夠較好地實現橡膠擠出機料筒溫度的精準控制。
參考文獻:
[1] 王文昌. 影響精密擠出穩定性的因素分析[J]. 化工管理,2015( 10) : 186-187.
[2] 孫若武.橡膠擠出機溫度壓力控制系統的研究[D]. 沈陽: 東北大學,2014.
[3] 張臨松,王士軍,陳偉,等. 塑料擠出機的多路溫度控制系統設計[J].自動化與儀表,2018,33(11) : 29-32.
[4] 李曉林.單螺桿精密擠出機理的研究[D]. 北京: 北京化工大學,2003.
[5]邊志堅.模糊 PID 在鑄錠爐溫控系統中的應用研究[D].石家莊: 河北科技大學,2015.
[6] 李全俊,黃權,李錦. Smith 預估模糊自適應 PID 控制在時滯系統中的應用[J]. 兵工自動化,2011,30(12) : 49-52.
[7] 高錦,章家巖,馮旭剛,等.基于失配補償 Smith-RBF神經網絡的主蒸汽壓力控制技術[J]. 重慶大學學報,2019,42( 7) : 105-113.
[8] 劉晴,李鴻.基于 Smith 預估模型+模糊 PID 的地鐵列車空調控制[J].工業控制計算機,2019,32(11) : 95-96.
[9] 王大志.面向實際工程問題的粒子群優化算法應用技術的研究[D].沈陽: 東北大學,2009.
[10] 史峰,王輝,郁磊. MATLAB 智能算法 30 個案例分析[M].北京: 北京航空航天大學出版社,2011.
[11] 張慶科.粒子群優化算法及差分進行算法研究[D]. 濟南: 山東大學,2017.
[12] 楊麗娟.熱電堆傳熱過程的數學建模與實踐[D].杭州:杭州電子科技大學,2015.
[13] 盛凱.冷喂料擠出機的溫度控制系統[J]. 橡塑技術與裝備,2001,27(11) : 52-54.
[14] 趙金龍.銷釘式冷喂料擠出機供膠系統在輪胎鋼絲簾布壓延中的應用[J].橡膠科技,2016,14(6) : 39-42.
[15] 陳超,陳樂庚,譚開順,等.橡膠冷喂料擠出機綜合控制方法[J].橡膠工業,2012,59(10) : 626-630.